1. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
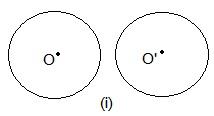
In these two circles, no point is common.
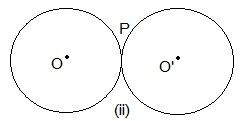
Here, only one point “P” is common.
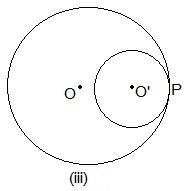
Even here, P is the common point.
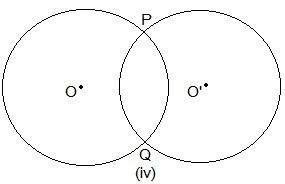
Here, two points are common which are P and Q.
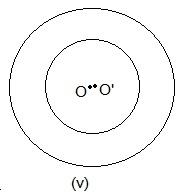
No point is common in the above circle.
2. Suppose you are given a circle. Give a construction to find its centre.
Solution:
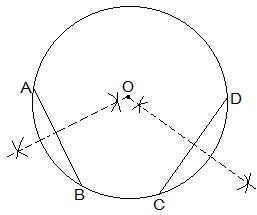
The construction steps to find the center of the circle are:
Step I: Draw a circle first.
Step II: Draw 2 chords AB and CD in the circle.
Step III: Draw the perpendicular bisectors of AB and CD.
Step IV: Connect the two perpendicular bisectors at a point. This intersection point of the two perpendicular bisectors is the centre of the circle.
3. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
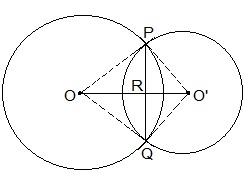
It is given that two circles intersect each other at P and Q.
To prove:
OO’ is perpendicular bisector of PQ.
Proof:
Triangle ΔPOO’ and ΔQOO’ are similar by SSS congruency since
OP = OQ and O’P = OQ (Since they are also the radii)
OO’ = OO’ (It is the common side)
So, It can be said that ΔPOO’ ΔQOO’
∴ POO’ = QOO’ — (i)
Even triangles ΔPOR and ΔQOR are similar by SAS congruency as
OP = OQ (Radii)
POR = QOR (As POO’ = QOO’)
OR = OR (Common arm)
So, ΔPOR ΔQOR
∴ PRO = QRO
Also, we know that
PRO+QRO = 180°
Hence, PRO = QRO = 180°/2 = 90°
So, OO’ is the perpendicular bisector of PQ.