NCERT Solutions For C lass 9 Math Chapter – 11 Exercise – 11.1

NCERT Solutions For Class 9 Math Chapter – 11 Constructions helps students in learning basic concepts of probability which is include in the second term’s CBSE syllabus 2021-2022  NCERT Solutions For Class 9 Maths provide answers to all the questions in exercise present at the end of the chapter These solutions are prepared by our mathematics experts who are highy experienced in the field of education.

 Experts at Sunstarup  have created the NCERT Solutions after extensive search on each topic Students can refer to this study study material to boost their confidence and attempt the second term exam smartly. The concepts are explained with steps, shortcuts to remember formula , tips and tricks to solve the numerical problems wisely and quickly.

 

1. Construct an angle of 90° at the initial point of a given ray and justify the construction.

Construction Procedure:

To construct an angle 90°, follow the given steps:

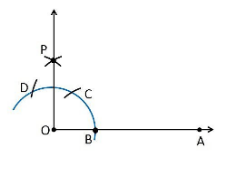
1. Draw a ray OA

2. Take O as a centre with any radius, draw an arc DCB is that cuts OA at B.

3. With B as a centre with the same radius, mark a point C on the arc DCB.

4. With C as a centre and the same radius, mark a point D on the arc DCB.

5. Take C and D as centre, draw two arcs which intersect each other with the same radius at P.

6. Finally, the ray OP is joined which makes an angle 90° with OP is formed.

Justification

To prove ∠POA = 90°

In order to prove this, draw a dotted line from the point O to C and O to D and the angles formed are:

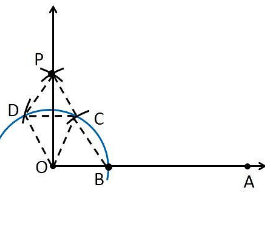
From the construction, it is observed that

OB = BC = OC

Therefore, OBC is an equilateral triangle

So that, ∠BOC = 60°.

Similarly,

OD = DC = OC

Therefore, DOC is an equilateral triangle

So that, ∠DOC = 60°.

From SSS triangle congruence rule

△OBC ≅ OCD

So, ∠BOC = ∠DOC [By C.P.C.T]

Therefore, ∠COP = ½ ∠DOC = ½ (60°).

∠COP = 30°

To find the ∠POA = 90°:

∠POA = ∠BOC+∠COP

∠POA = 60°+30°

∠POA = 90°

Hence, justified.

2. Construct an angle of 45° at the initial point of a given ray and justify the construction.

Construction Procedure:

1. Draw a ray OA

2. Take O as a centre with any radius, draw an arc DCB is that cuts OA at B.

3. With B as a centre with the same radius, mark a point C on the arc DCB.

4. With C as a centre and the same radius, mark a point D on the arc DCB.

5. Take C and D as centre, draw two arcs which intersect each other with the same radius at P.

6. Finally, the ray OP is joined which makes an angle 90° with OP is formed.

7. Take B and Q as centre draw the perpendicular bisector which intersects at the point R

8. Draw a line that joins the point O and R

9. So, the angle formed ∠ROA = 45°

Justification

From the construction,

∠POA = 90°

From the perpendicular bisector from the point B and Q, which divides the ∠POA into two halves. So it becomes

∠ROA = ½ ∠POA

∠ROA = (½)×90° = 45°

Hence, justified

Solution:

(i) 30°

Construction Procedure:

1. Draw a ray OA

2. Take O as a centre with any radius, draw an arc BC which cuts OA at B.

3. With B and C as centres, draw two arcs which intersect each other at the point E and the perpendicular bisector is drawn.

4. Thus, ∠EOA is the required angle making 30° with OA.

Construction Procedure:

1. Draw an angle ∠POA = 90°

2. Take O as a centre with any radius, draw an arc BC which cuts OA at B and OP at Q

3. Now, draw the bisector from the point B and Q where it intersects at the point R such that it makes an angle ∠ROA = 45°.

4. Again, ∠ROA is bisected such that ∠TOA is formed which makes an angle of 22.5° with OA

(iii) 15°

Construction Procedure:

1. An angle ∠DOA = 60° is drawn.

2. Take O as centre with any radius, draw an arc BC which cuts OA at B and OD at C

3. Now, draw the bisector from the point B and C where it intersects at the point E such that it makes an angle ∠EOA = 30°.

4. Again, ∠EOA is bisected such that ∠FOA is formed which makes an angle of 15° with OA.

5. Thus, ∠FOA is the required angle making 15° with OA.

4. Construct the following angles and verify by measuring them by a protractor:

(i) 75° (ii) 105° (iii) 135°

Solution:

(i) 75°

Construction Procedure:

1. A ray OA is drawn.

2. With O as centre draw an arc of any radius and intersect at the point B on the ray OA.

3. With B as centre draw an arc C and C as centre draw an arc D.

4. With D and C as centre draw an arc, that intersect at the point P.

5. Join the points O and P

6. The point that arc intersect the ray OP is taken as Q.

7. With Q and C as centre draw an arc, that intersect at the point R.

8. Join the points O and R

9. Thus, ∠AOE is the required angle making 75° with OA.

(ii) 105°

Construction Procedure:

1. A ray OA is drawn.

2. With O as centre draw an arc of any radius and intersect at the point B on the ray OA.

3. With B as centre draw an arc C and C as centre draw an arc D.

4. With D and C as centre draw an arc, that intersect at the point P.

5. Join the points O and P

6. The point that arc intersect the ray OP is taken as Q.

7. With Q and Q as centre draw an arc, that intersect at the point R.

8. Join the points O and R

9. Thus, ∠AOR is the required angle making 105° with OA.

(iii) 135°

Construction Procedure:

1. Draw a line AOA‘

2. Draw an arc of any radius that cuts the line AOA‘at the point B and B‘

3. With B as centre, draw an arc of same radius at the point C.

4. With C as centre, draw an arc of same radius at the point D

5. With D and C as centre, draw an arc that intersect at the point O

6. Join OP

7. The point that arc intersect the ray OP is taken as Q and it forms an angle 90°

8. With B‘ and Q as centre, draw an arc that intersects at the point R

9. Thus, ∠AOR is the required angle making 135° with OA.

5. Construct an equilateral triangle, given its side and justify the construction.

Construction Procedure:

1. Let draw a line segment AB = 4 cm .

2. With A and B as centres, draw two arcs on the line segment AB and note the point as D and E.

3. With D and E as centres, draw the arcs that cuts the previous arc respectively that forms an angle of 60° each.

4. Now, draw the lines from A and B that are extended to meet each other at the point C.

5. Therefore, ABC is the required triangle.

Justification:

From construction, it is observed that

AB = 4 cm, ∠A = 60° and ∠B = 60°

We know that, the sum of the interior angles of a triangle is equal to 180°

∠A+∠B+∠C = 180°

Substitute the values

⇒ 60°+60°+∠C = 180°

⇒ 120°+∠C = 180°

⇒∠C = 60°

While measuring the sides, we get

BC = CA = 4 cm (Sides opposite to equal angles are equal)

AB = BC = CA = 4 cm

∠A = ∠B = ∠C = 60°

Hence, justified.